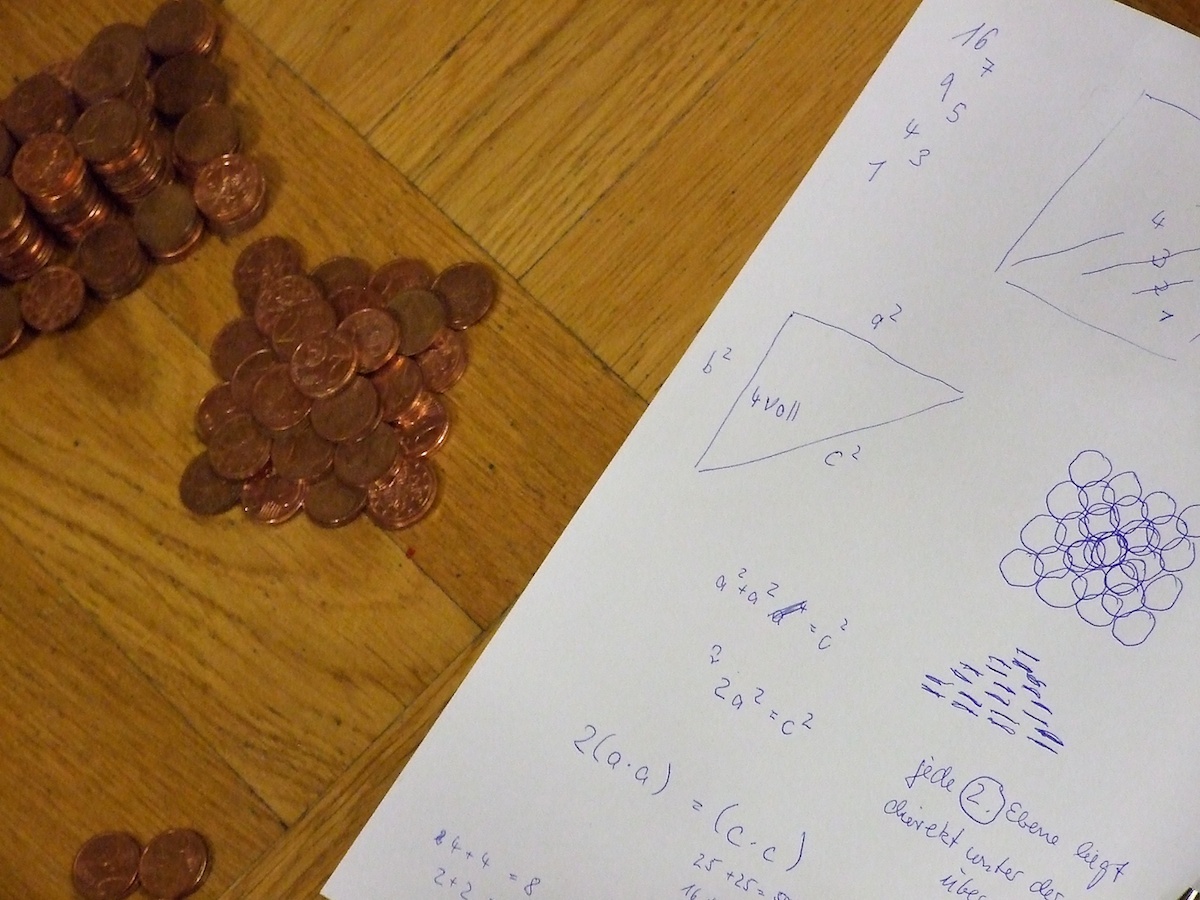Workshop 3
Kompetenzen erwerben! Wie Lernen lebensnah wird.
Referentinnen und Referenten:
Workshop beim 10. Ganztagsschulkongress
Freitag, 06.12.2013, 13:30–15:30 Uhr, Raum A 04
Dr. Kerstin Tschekan, Institut für Qualitätsentwicklung an Schulen Schleswig-Holsteins, Sachgebietsleiterin Fächer, Fachrichtungen und Fachberatung; Oberschule Helgolander Straße, Bremen
Wie müssen handlungsorientierte Lernsituationen gestaltet sein, damit alle Schülerinnen und Schüler lernen können?
Wie können Lehrkräfte ihre Rolle zwischen dem Begleiten des selbstständigen Lernens und dem Vermitteln von Struktur erfüllen?
Wie müssen Lernarrangements aussehen, damit Methoden zu mehr Lernerfolg führen?
Dr. Kerstin Tschekan, Institut für Qualitätsentwicklung an Schulen Schleswig-Holstein. Sie setzt sich für einen „neuen Geist“ in der Schule ein. Angeleitet von Begleitpersonen sollen sich die Schülerinnen und Schüler selbstständig ihre Kompetenzen aneignen können.
Thomas d’Hénin und Michael Rohdenburg, Oberschule Helgolander Straße, Bremen. Der Fachsprecher Mathematik und der Ganztagskoordinator schilderten die Methode des forschend-entdeckenden Lernens, mit der ihre Schülerinnen und Schüler mathematische Phänomene in ihrer Lebenswelt erkunden.
Moderation: Tanja Klockmann, Serviceagentur „Ganztägig lernen“ Schleswig-Holstein, und Christina Tietjen, Serviceagentur „Ganztägig lernen“ Bremen
Zentrale Themen und Ergebnisse
Einstieg in Murmelgruppen: Was machte für Sie als Lernende guten Mathematikunterricht aus? Wodurch zeichneten sich erfolgreiche Lernsituationen aus?
Es war ein sehr angeregter Austausch.
Ablauf
- Präsentation der Referenten (siehe unten [PDF]) zum Ansatz des forschenden Lernens in der Mathematik: Was ist das und wie grenzt es sich von anderen Unterrichtskonzepten (Projektlernen, problemorientiertes Lernen) ab?
- Arbeitsphase (eine Stunde): Die Teilnehmer sollen in Kleingruppen “Mathematik erfinden”, und zwar mit Material (Holzwürfel und Cent-Stücke) etwas bauen, Forscherfragen entwickeln und beantworten.
- Auswertung und Reflexion: Es werden anhand von Fotos der entstandenen Bauwerke (siehe Bild) einige Bauwerke und Forscherfragen vorgestellt.
1. Beispiel “Holzwürfel”
- Zwei Gebäude aus Holzwürfeln sind zu sehen, und die Gruppe überlegt, welche Gebäude es sein könnten.
-
Fragen an die Baugruppe: Welche mathematischen Fragen haben Sie in Ihrem Gebäude entdeckt bzw. daran diskutiert?
- Wie viele Steine wurden verbaut? → Wie könnte man diese Frage beantworten? Jetzt sind wir mitten in der Mathematik, und es werden Lösungsmodelle vorgeschlagen und diskutiert (Würfel zählen, Kantenwürfel zählen und multiplizieren)
- Wie groß ist die Grundfläche des Bauwerkes? Deutlich wird: Mehrere Lösungswege können zum Ziel führen.
- Welches Bauwerk ist höher? Wie viel höher als das andere ist es?
Referenten: “Wie ist es Ihnen mit dem Doku-Auftrag ergangen?”
Die Referenten kommentieren ihr Vorgehen im Workshop so, dass deutlich wird, wie sie konkret mit den Schülerinnen und Schülern dazu arbeiten würden:
- “Wir lassen die gestellten Fragen nicht unbeantwortet, sondern sorgen dafür, dass es Raum und Zeit gibt, die aufgekommenen Fragen auch zu beantworten.”
- “Wir arbeiten in Doppelstunden. So gibt es auch Zeit für Dokumentation.”
- “In der 1. Stunde sind die Schülerinnen und Schüler sehr, sehr kreativ. Später – auch durch die Dokumentation – kommt dann zwangsläufig eine Präzision dazu, denn schräg aufeinander stehende Steine kann man schlechter zählen bzw. abzeichnen. Dann korrigieren die Schüler manchmal ihr Bauwerk, um besser zählen zu können.” (Referent)
2. Beispiel “Münzen”
Zu sehen sind eine Art Halbkugel sowie eine “Linie” aus Münzen.
- Welche mathematischen Fragestellungen verbergen sich dahinter?
- Ab wann stehen die Münzen wieder genau aufeinander?
- Inwieweit nimmt die Anzahl der Münzen auf einer Ebene weiter zu?
Referent: “Unsere Schüler üben an solchen Figuren gern das Schätzen: Wie viele Würfel werden wir für das Gebäude brauchen? Das ist ein Ansatz, der in Klasse 2 und in Klasse 10 funktioniert, wenn auch die mathematischen Lösungsansätze andere sind.”
3. Beispiel “Labyrinth”
Fragen einer Teilnehmerin: Wie kann es jetzt konkret im Mathematikunterricht eingesetzt werden? Wie geht es im Unterricht nach dem Bauen weiter?
Antwort: Eine solche Sequenz dauert 4 Mathematikstunden: bauen, dokumentieren, diskutieren, rechnen, auswerten.
- “Das Tolle: Man schneidet ganz viele Themen der Mathematik an! Und zwar nebenbei. Die Schülerinnen und Schüler merken manchmal gar nicht, dass sie über Mathematik reden, obwohl sie die ganze Zeit über ihr Gebäude mit Begriffen wie Symmetrie, Achsen und Auszählen arbeiten. So holt man die Kinder wirklich da ab, wo sie sind. Sie werden aktiviert und bringen das ein, was sie können.”
- “Die Konzentration ist enorm bei diesem praktischen Tun. In einer solchen Stunde machen die Kinder tatsächlich 89 von 90 Minuten Mathematik – das gelingt mir in anderen Lernsituationen nicht!”
Frage einer Teilnehmerin: “Wie schaffe ich es mit der Methode „Forschendes Lernen“ die Themen des Rahmenlehrplans abzudecken?”
Referent: “Sie kommen auf ganz viele Themen aus dem Rahmenlehrplan – nur bestimmen Sie als Lehrer nicht den Zeitpunkt, in welcher Stunde welches Thema bearbeitet wird, sondern die Schülerinnen und Schüler. Aber das ist mir egal. Hauptsache ist, sie machen diese mathematischen Erfahrungen! Und: Wir arbeiten nicht durchgehend das ganze Schuljahr mit dieser Methode. Das dauert höchstens vier Wochen und dann kommen wieder andere Arbeitsformen.”
Kommentar einer TN: Hilfreich für die Praxis wäre, die zu entwickelnden Kompetenzen zu erfassen und zu visualisieren. An meiner Schule ist es ein “Baum” für die Klasse, an den nach und nach bunte Zettel mit den Fähigkeiten aufgehängt wurden, die die Schülerinnen und Schüler im Lauf der Zeit erworben haben. Nach einer gewissen Zeit ist dieser Baum ziemlich voll und bunt und man kann rekapitulieren, was alles schon gelernt wurde.
Abschlussphase: Welche Chancen sehen Sie im Konzept und wo sehen Sie Schwierigkeiten und Bedenken?
- “Ich habe Bedenken, dass es mir in der Praxis schwer fällt, darauf zu vertrauen, dass die Kinder einen Plan haben und schon wissen, was sie tun wollen und können.”
- “Manche Klassen sind ja sehr anstrengend. Gerade mit solchen Arbeitsformen entstehen ja noch mehr Konflikte. Wie kann damit umgegangen werden?”
- Ein anderer Lehrer reagiert darauf: “Wenn Kinder etwas finden, was sie interessiert und sie leidenschaftlich damit arbeiten, sind sie ja nicht mehr anstrengend – das ist ja das Tolle!”
- “Man spricht zu viele Themen der Mathematik gleichzeitig an. Überfordert das nicht die Schüler? Ich wüsste dann gar nicht, woran in der Tiefe weiter zu arbeiten ist? Nur an der Oberfläche kratzen ist ja unbefriedigend!”
- “Was ist, wenn Schülerinnen und Schüler mehr entdecken, als sie fachlich wissen, also Fragen entwickeln, die sie mathematisch noch gar nicht erschließen können? Wie organisiert man das?”
- Referent: “Das ist ja der Ausgangspunkt, sich die Formel dann zu erarbeiten.”
- “Diese Methode weist sehr schön den Weg zum kompetenzorientierten Lernen. Es ist natürlich nicht die einzige Methode. Es braucht Erkundungs- und Übungsphasen im Wechsel.”
- Frage an Schülerinnen und Schüler: Wie attraktiv wäre der Ansatz für euch?
- Antwort: “Wir sind jetzt in einem Alter (habe gerade mein Abitur gemacht), in dem man sich schlecht auf eine neue Lernformen einlassen kann. So zu arbeiten, dass es nicht darum geht, einen Lösungsweg nachzuvollziehen, sondern zuerst ein Problem zu erkennen und dann eine Lösung zu entdecken und eine Antwort zu finden, fiele mir heute einerseits schwer, andererseits war Mathematik immer nicht mein Fach und ich hätte mit dieser Methode sicher besser lernen können.”
- “Ist das nicht für Ältere zu spielerisch?”
- Referent: “Die Schülerinnen und Schüler entscheiden ja selbst, woran sie arbeiten. Sie würden nicht das bearbeiten, was sie schon wissen, wo sie keine Fragen mehr haben, sondern das, was für sie fragwürdig ist. Darüber kommt auch Begeisterung”
- “Wenn damit etwas Begeisterung für Mathematik geweckt ist, dann ist doch schon viel erreicht!”
- Schüler reagiert: “Ja, aber es frustriert auch, wenn auftauchende Fragen nicht beantwortet werden (können).”
- Referent: “Wichtig ist der Punkt, dass die Schülerinnen und Schüler Lösungen suchen und ggf. scheitern. Aber nicht etwa der Lehrer sagt, dass er es nicht rausfinden kann. So entsteht keine Frustration. Ich habe zumindest noch keine erlebt.”
- Teilnehmer aus dem Workshop: “Wenn man den Schülern die Zeit und die Unterstützung gibt, diese Themen und Formeln dann zu erschließen und wenn dann ein Schüler viel früher, als der Rahmenlehrplan es vorsieht, die Pyramidenformel lernt, ist das doch großartig!”
- “Das Material ist übrigens austauschbar. Sie können auch Wäscheklammern oder Gummibärchen nehmen!”
Statements und Zitate
- Referent Thomas d`Hénin: “Auf das aktivierende Material kommt es an. Bei uns ist es manchmal so, dass Schülerinnen und Schülern schon sieben Minuten vor Unterrichtsbeginn mit dem Material umgehen und kaum zu bremsen sind. Sie wollen einfach damit tun!”
- Lehrer: “Mir leuchtet ein, dass es emotional beeindruckend ist, wenn ein Schüler eine Brücke selber nachbaut, die eine komplizierte Architektur hat, aber warum die dann trägt, weiß er deshalb ja noch nicht – das fehlt mir dann noch und muss auch thematisiert werden.”